いろはにほへと

元証券アナリストのひとりごと

株はゼロサムゲーム？　プラスサムゲームなら必ず儲かる？

資産運用

Twitterで盛り上がっている、株はゼロサムゲームなのかプラスサムゲームなのか論争。

ずーっと眺めていて思ったこと。

それは、みんな、ゼロサムゲームの意味、勘違いしてない？ってことでした。

株はゼロサムゲームなのか、もしプラスサムゲームと言えるなら必ず儲かるものなのか、そのあたりについてまとめてみました。

 

 

そもそもゼロサムってなによ？

ゼロサムゲームのサムはSUM関数のサムです。

つまり合計という意味です。

ゼロサムゲームのゼロは数字の０です。

 

たとえば、AさんとBさんが賭けをしていて、勝った方が１００円もらい、負けたほうが１００円払う場合、ゼロサムゲームと言えます。

これは、買った方が＋１００円、負けたほうが△１００円なので、合計すると０円になるからです。

 

このようにゲーム理論という数学なので、定義が決まっています。

「誰かから見ればゼロサムに見えて、誰かから見ればプラスサムに見える」という理屈はありえません。

 

ということはプラスサムってなに？

で、プラスサムはというと、もうお分かりだと思います。

さきほどの例で言うと、買った方が１００円もらい、負けたほうが５０円払う場合、プラスサムゲームになります。

１００円ー５０円＝５０円なので、合計すると５０円になりますよね。

５０というのは正の数なのでプラス。

なのでプラスサムゲームというわけです。

 

プラスサムなら必ず儲かるの？

Twitterで見ていて思ったのは、「株はプラスサムゲームだけど、全員が儲かるわけではない」ということが分かっていない人も案外多いってことです。

 

プラスサムは必ず儲かるわけではありません。

さきほどの例で示した通り、片方が得をし、片方が損をする場合でも、プラスサムゲームは成立するからです。

たとえば１０人で賭けをして、１位だけ10,000円、２位以下は500円損をするゲームでも、10,000円－（500円×９人）＝5,500円なので、プラスサムゲームと言えます。

１０人中９人が損をしてもそれはプラスサムゲームであり、どれくらいの割合の人が損をしたかは全く関係ないのです。

 

 

平均がプラスなら、合計もプラス

話はちょっと変わりますが、合計と平均の関係には以下のような性質があります。

平均がプラスであれば、合計がプラス。

平均がマイナスであれば、合計はマイナス。

平均が０であれば、合計は０になります。

 

これは、合計をA、割る数をBとした場合、平均はA／Bとなりますが、Bは必ずプラスの数なので、A／BはAが正の数か負の数かに依るからです。

ちなみに０の時は０になります。

まあ感覚的に分かると思いますが。。

 

平均株価はプラスなので、プラスサムゲーム

さて、なんでそんな話を持ってきたのかというと、株はゼロサムかプラスサムかという話になると、絶対にプラスサムであるという論拠になるからです。

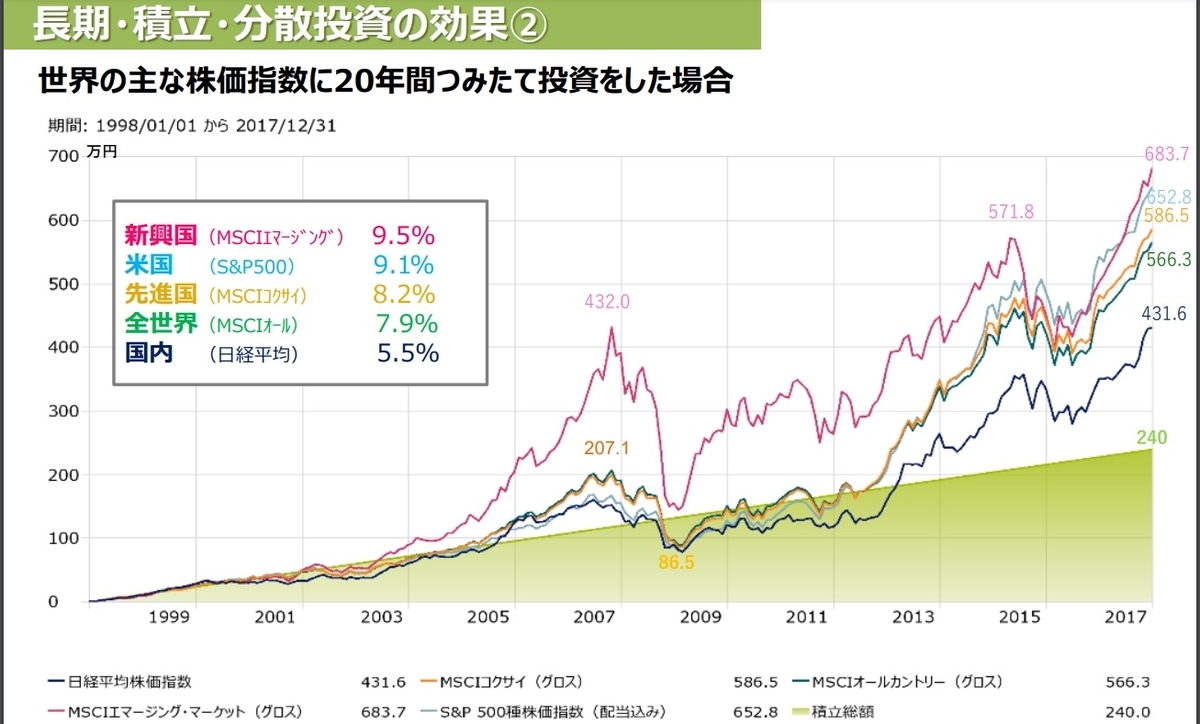
上の表は各国の平均株価に毎月積み立てた場合のグラフです。

さきほど、平均と合計の関係性についてお話ししましたが、「平均」株価がプラスなので、株はプラスサムゲームと言えるのです。

ただし、ここで間違えていただきたくないのは、「プラスサム」は全員が儲かっているという意味ではないという点です。

あくまで、合計するとプラスなだけであって、ひょっとしたら１０人中９人は損をしている・・という可能性がないわけではありません。

そういう証拠も特にありませんが。