因数分解は中学数学において一気に難易度が上がる分野です。
ここで躓いてしまう方も多い(多かった)のではないでしょうか。
そもそも数式をいじってるだけでなんだか抽象的で、何をやってるのか分かりにくいのが原因かもしれません。
でも、因数分解は図形とグラフで考えると一気にわかりやすくかつ面白くなります。
因数分解とは?
数学における因数分解(いんすうぶんかい、英: factorization, factoring, decomposition[注釈 1]; 分解、因子分解)は、与えられた数学的対象を同種の(しかし普通はより小さいあるいはより平易な)別の対象—それは因数(factor; 因子、乗法因子、乗因子)と呼ばれる—の積として書き表すことを言う[注釈 2]。たとえば、15 という項数は 3 × 5 という因数の積に分解され、他項式 x2 − 4 は (x − 2)(x + 2) という因数の積に分解される。(Wikipediaより)
中学3年生の因数分解は一つの長方形にまとめること
正直なんだかわかりにくい説明がWikipediaには書いてありますが、実は、中学3年生で習う因数分解は、ばらばらの長方形を1つの長方形にするという考え方ですべて説明することができます。
※今回、正方形は長方形の一種のため、正方形も長方形と呼びます※
たとえば、a^2+2ab+b^2という式を因数分解する場合を考えてみましょう。
※表記注※ a^2=a2
a^2+2ab+b^2は以下のような長方形(今回は正方形も長方形の一種と考え、長方形と表記します)の集まりと考えることができます。
- a^2という一辺がaである長方形が1つ
- abという縦がa横がbである長方形が2つ
- b^2という一辺がbである長方形が1つ
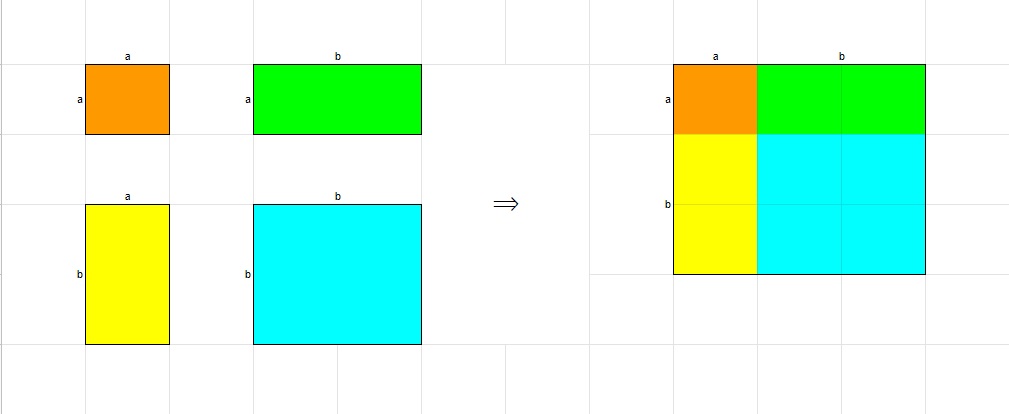
上記を図に書きだすと、下左図のようになり、これを1つの長方形にまとめると下右図のようになります。
右図は縦が(a+b)、横が(a+b)の長方形なので、面積は(a+b)^2となります。
これはa^2+2ab+b^2の因数分解の答えと同じになります。
a^2+2ab+b^2=(a+b)^2
マイナスの概念が出てくる場合はグラフに当てはめればok
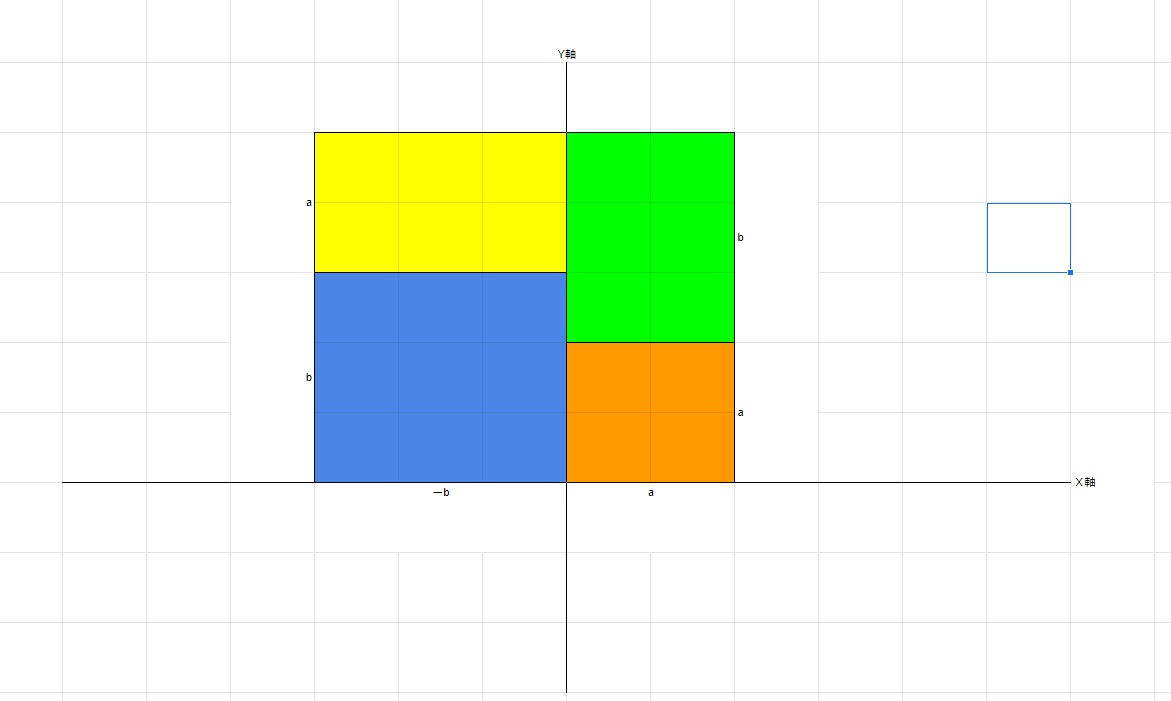
次に、a^2‐2ab+b^2=(a‐b)^2という因数分解を考えてみましょう。
先ほどと同じように長方形の集まりについて考えてみると、
- a^2という一辺がaである長方形が1つ
- ‐abという縦がa横がbである長方形が2つ
- b^2という一辺がbである長方形が1つ
となります。
困るのが、面積が‐abという長方形・・そんな面積がマイナスになる長方形なんてこの世に存在しませんよね。
でも、数学の世界ではそういう長方形を作り出すことができます。
その道具がグラフです。
下の図のように、グラフ上に長方形を書けば、面積がマイナスになる長方形を描くことができます。
今回の場合で言えば、黄色と緑の長方形は一辺がマイナスでもう一辺がプラスなので、面積はマイナスになります。
ちなみに、青のところに面積がb^2の長方形を書きたくなりますが、ブルーのところにもb^2の長方形を書くことができます。(両辺がマイナスなので、掛け算をすると面積はプラスになる)
出来上がった長方形の一辺は(a‐b)となりますので、面積は(a‐b)^2となります。
四角形を補完して考えることもOK
では、最後にもっとも難しい公式を考えてみましょう。
a^2‐b^2=(a+b)(a‐b)
この場合、まず先ほどまでと同じように長方形になおすと以下のようになります。
- a^2という一辺がaである長方形が1つ
- ‐b^2という一辺がbである長方形が1つ
オレンジと青の長方形しかない為、一つの長方形にならないですね。
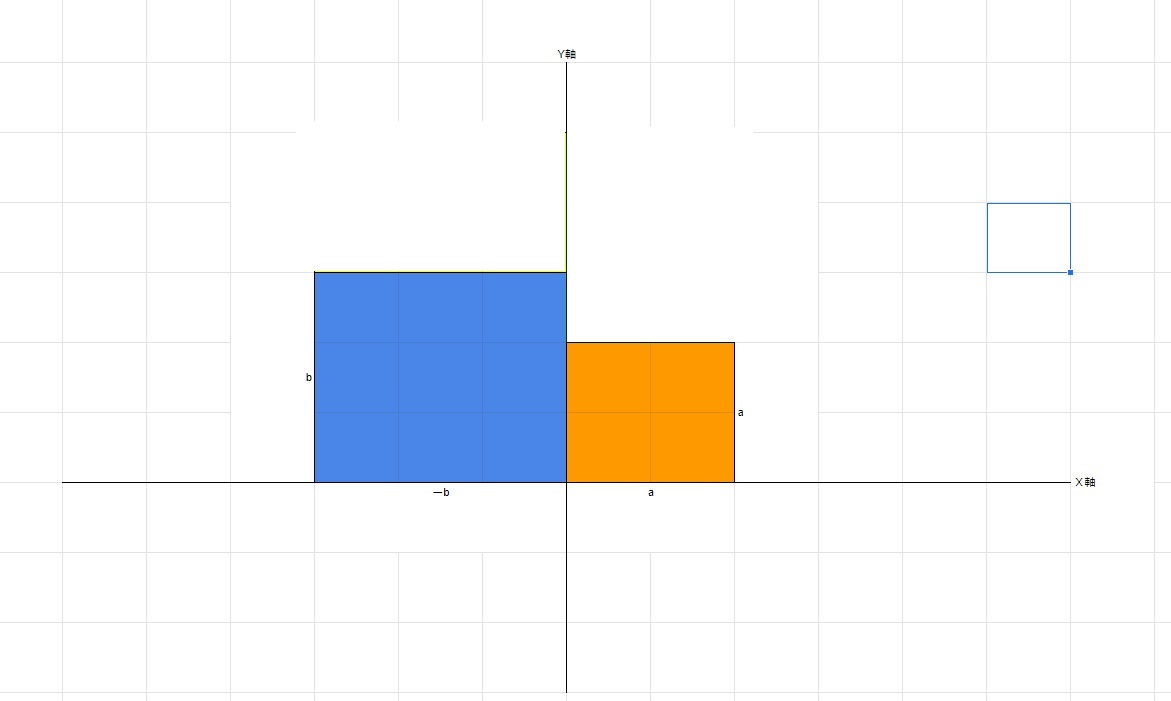
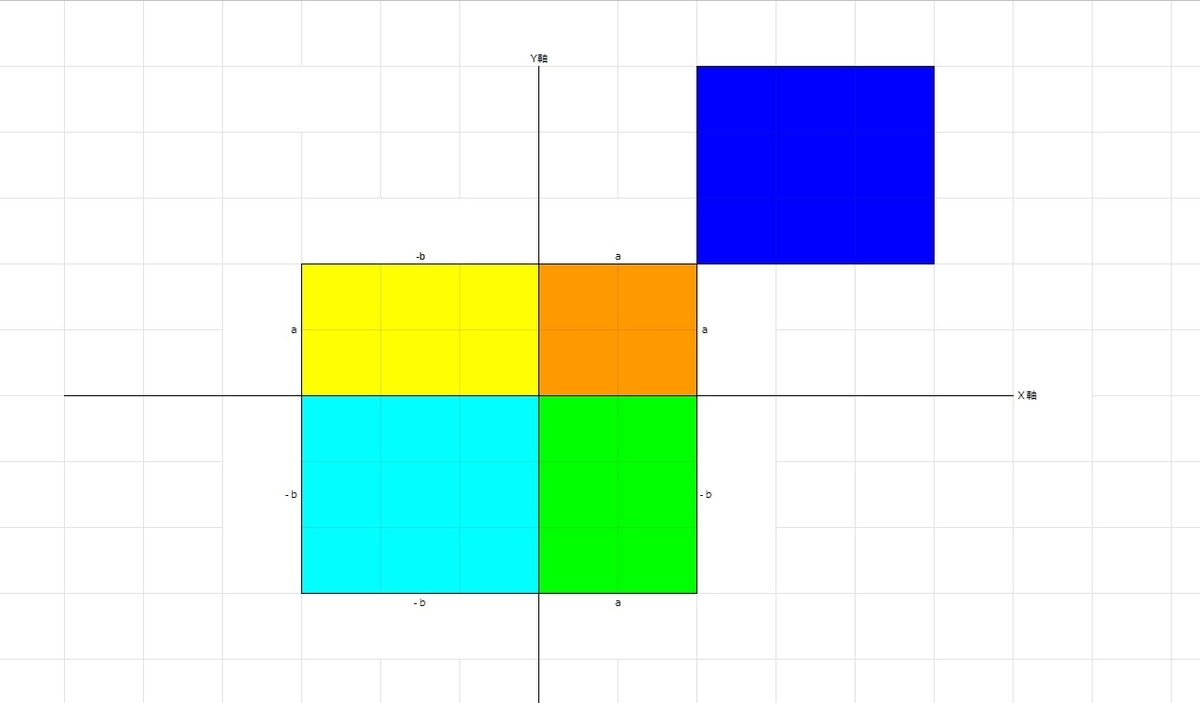
そのため、下図のように、黄色と緑の長方形を補完して、一つの長方形を作り出します。
黄色の長方形と緑の長方形は同じ面積で、黄色の長方形の面積は‐ab、緑色の長方形の面積はabとなります。
なので、黄色と緑は付け足しても面積が増えるわけではないので(黄色の面積が‐ab、緑色の面積がabで、合計が0になるので)補完してもOKなわけですね。
※合計して0になるようにしないと、数字を増加させたことになる※
下図のように、一辺が(a+b)もう一辺が(a‐b)となる長方形が出てきましたね。